Aceasta este Partea 2 dintr-o serie de articole axate pe proprietățile și aplicațiile rețelelor neurale convoluționale (CNN), utilizate în principal pentru recunoașterea modelelor și clasificarea obiectelor. În primul articol, „Introducere în rețelele neuronale convoluționale: Ce este învățarea automată? – Partea 1”, am arătat cum diferă execuția unui program liniar clasic pe un microcontroler de funcționarea unei rețele CNN și care sunt avantajele acesteia. A fost prezentată, de asemenea, rețeaua CIFAR, utilizată pentru clasificarea obiectelor precum pisici, case sau biciclete în imagini, precum și pentru realizarea unor sarcini simple de recunoaștere a modelelor vocale.
Partea 2 explică modul în care aceste rețele neuronale pot fi antrenate pentru a rezolva astfel de probleme.
Procesul de antrenare a rețelelor neurale
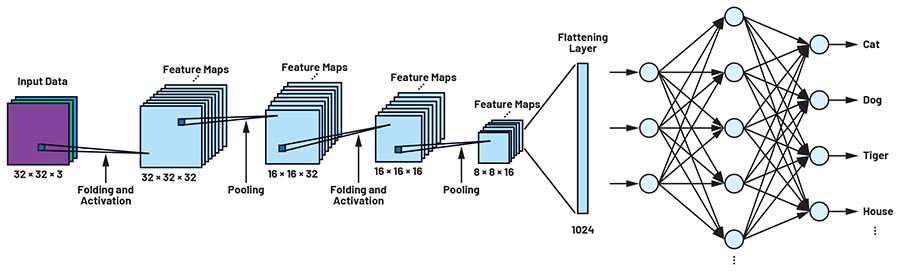
Rețeaua CIFAR, prezentată în prima parte a seriei, este alcătuită din diferite straturi de neuroni, așa cum se poate observa în Figura 1. Imagini de 32 × 32 pixeli sunt prezentate rețelei și propagate prin straturile acesteia. Primul pas într-o rețea CNN constă în detectarea și analiza caracteristicilor și structurilor distinctive ale obiectelor care trebuie diferențiate. În acest scop sunt utilizate matrici de filtrare.
Odată ce o rețea neurală, precum CIFAR, a fost definită de un proiectant, aceste matrici de filtrare sunt inițial necunoscute, iar rețeaua nu este încă capabilă să detecteze modele și obiecte.
Antrenarea rețelelor CNN prin optimizarea funcției de pierdere
Pentru a permite acest lucru, este necesar să se determine toți parametrii și elementele matricilor astfel încât să fie maximizată precizia detectării obiectelor sau, echivalent, să fie minimizată funcția de pierdere. Acest proces este cunoscut sub numele de antrenarea rețelei neurale. Pentru aplicațiile uzuale descrise în prima parte a seriei, rețelele sunt antrenate o singură dată în faza de dezvoltare și testare. Ulterior, ele sunt gata de utilizare, iar parametrii nu mai trebuie ajustați. Dacă sistemul clasifică obiecte deja cunoscute, nu este necesar un antrenament suplimentar; acesta devine necesar doar atunci când trebuie clasificate obiecte complet noi.
Datele de antrenare sunt necesare pentru a instrui o rețea, iar ulterior un set similar de date este utilizat pentru a testa precizia acesteia. În cazul setului de date CIFAR-10, de exemplu, imaginile sunt organizate în zece clase de obiecte: avion, automobil, pasăre, pisică, cerb, câine, broască, cal, navă și camion. Însă – și aceasta reprezintă una dintre cele mai complexe etape ale dezvoltării unei aplicații AI – aceste imagini trebuie etichetate înainte de antrenarea unei rețele CNN.
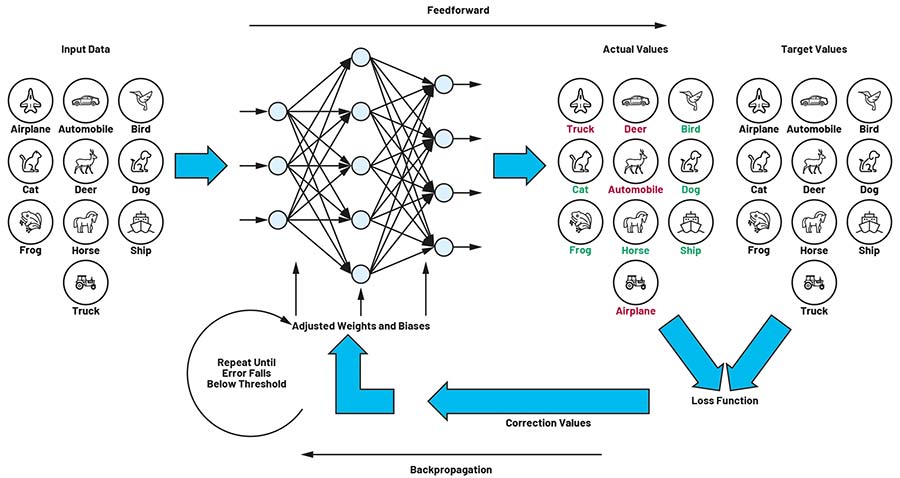
Figura 2: Buclă de antrenare formată din propagare directă (feedforward) și retropropagare (backpropagation). (Sursa imaginii: Analog Devices)
Procesul de antrenare, descris în acest articol, se bazează pe principiul retropropagării (backpropagation). Rețelei i se prezintă succesiv un număr mare de imagini, fiecare fiind însoțită de o valoare țintă. În exemplul nostru, această valoare reprezintă clasa de obiect asociată imaginii. De fiecare dată când este prezentată o imagine, matricile de filtrare sunt ajustate astfel încât valorile calculate să se apropie cât mai mult de valorile țintă. După finalizarea acestui proces, rețeaua este capabilă să detecteze și să clasifice obiecte din imagini pe care nu le-a întâlnit în timpul antrenării.
Supraajustare și subajustare
În modelarea rețelelor neurale apar frecvent întrebări legate de complexitatea rețelei: câte straturi ar trebui să aibă și cât de mari ar trebui să fie matricile de filtrare. Nu există un răspuns simplu sau universal la aceste întrebări. În acest context, este important să discutăm conceptele de supraajustare (overfitting) și subajustare (underfitting) ale rețelelor neurale.
Supraajustarea este rezultatul unui model excesiv de complex, care conține prea mulți parametri. Putem evalua dacă un model de predicție este insuficient ajustat sau, dimpotrivă, supraajustat, comparând pierderea obținută pe datele de antrenare cu pierderea obținută pe datele de testare. Dacă pierderea este redusă în timpul antrenării, dar crește semnificativ atunci când rețeaua este evaluată cu date de testare pe care nu le-a întâlnit anterior, acesta este un indiciu clar că rețeaua a memorat datele de antrenare, în loc să generalizeze recunoașterea modelelor.
Acest fenomen apare, în principal, atunci când rețeaua dispune de prea mult spațiu pentru parametri sau de un număr excesiv de straturi de convoluție. În astfel de cazuri, dimensiunea și complexitatea rețelei ar trebui reduse.
Funcția de pierdere și algoritmii de antrenare
Învățarea are loc în două etape. În prima etapă, rețelei i se prezintă o imagine, care este procesată de rețeaua neurală pentru a genera un vector de ieșire. Valoarea maximă din acest vector reprezintă clasa de obiecte detectată, de exemplu un câine în cazul nostru, care, în faza de antrenare, nu trebuie să fie neapărat corectă. Această etapă este denumită feedforward.
Diferența dintre valorile țintă și valorile reale obținute la ieșire este denumită pierdere, iar funcția care descrie această diferență este funcția de pierdere. Toți parametrii și elementele rețelei sunt incluși în această funcție. Scopul procesului de învățare al rețelei neurale este de a ajusta acești parametri astfel încât funcția de pierdere să fie minimizată.
Minimizarea se realizează printr-un proces în care eroarea de la ieșire (pierdere = valoarea țintă minus valoarea reală) este propagată înapoi prin toate straturile rețelei, până la stratul inițial. Această etapă a procesului de învățare este cunoscută sub denumirea de propagare înapoi (backpropagation).
În timpul antrenării se formează astfel o buclă iterativă care ajustează treptat parametrii matricilor de filtrare. Procesul de propagare înainte și înapoi se repetă până când valoarea pierderii scade sub un prag definit anterior.
Algoritmul de optimizare, gradientul și metoda de coborâre a gradientului
Pentru a ilustra procesul de antrenare, figura 3 prezintă o funcție de pierdere definită doar de doi parametri, x și y. Axa z corespunde valorii pierderii. Funcția în sine nu joacă un rol esențial aici și este utilizată exclusiv în scop ilustrativ. Analizând graficul funcției tridimensionale, se poate observa că aceasta prezintă atât un minim global, cât și minime locale.
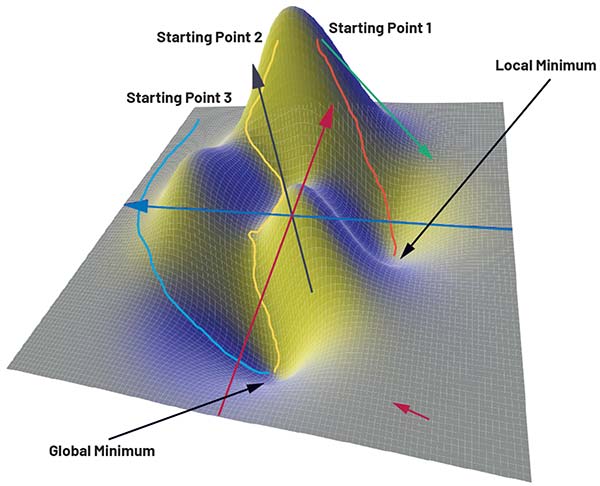
Figura 3: Diferite căi către țintă folosind metoda de coborâre a gradientului. (Sursa imaginii: ADI)
Pentru determinarea ponderilor și a biasurilor pot fi utilizați numeroși algoritmi de optimizare numerică. Cel mai simplu dintre aceștia este metoda de coborâre a gradientului. Aceasta se bazează pe ideea de a găsi o cale, pornind dintr-un punct ales aleatoriu în funcția de pierdere, care conduce către minimul global, printr-un proces iterativ ghidat de gradient.
Gradientul, ca operator matematic, descrie variația unei mărimi și furnizează, în fiecare punct al funcției de pierdere, un vector – numit vector gradient – care indică direcția celei mai mari creșteri a valorii funcției. Modulul acestui vector corespunde amplitudinii variației. În funcția ilustrată în figura 3, vectorul gradient ar indica direcția de coborâre către un minim, de exemplu în zona din dreapta jos (săgeata roșie), unde suprafața este relativ plată și magnitudinea gradientului este mică. În apropierea vârfului, în schimb, vectorul (săgeata verde) indică o pantă abruptă, având o magnitudine mai mare.
Limitările metodei clasice de coborâre a gradientului
Utilizând metoda de coborâre a gradientului, algoritmul caută în mod iterativ o cale care conduce către cea mai abruptă scădere, pornind dintr-un punct ales arbitrar. Acesta calculează gradientul în punctul de pornire și efectuează un pas mic în direcția de coborâre maximă. În punctul următor, gradientul este recalculat, iar procesul continuă până când se ajunge într-o zonă de minim.
Problema este că punctul de pornire nu este definit în prealabil, ci este ales aleatoriu. În exemplul bidimensional din figura 3, un punct de pornire ales în partea stângă a graficului poate conduce la minimul global (traseul albastru), în timp ce alte puncte pot duce la trasee mai lungi sau la minime locale (traseele galben și portocaliu).
În practică, această abordare devine problematică deoarece algoritmul trebuie să optimizeze nu doar doi parametri, ci adesea sute de mii sau milioane. Alegerea unui punct de pornire favorabil este, astfel, pur întâmplătoare. Ca urmare, timpul de antrenare poate crește semnificativ, iar rețeaua poate converge către un minim local, ceea ce duce la o precizie redusă.
Din acest motiv, în ultimii ani au fost dezvoltați numeroși algoritmi de optimizare care încearcă să evite aceste limitări. Printre aceștia se numără metoda de coborâre a gradientului stochastic, momentum, AdaGrad, RMSProp și Adam. Alegerea algoritmului potrivit este lăsată la latitudinea dezvoltatorului, deoarece fiecare metodă prezintă avantaje și dezavantaje specifice, în funcție de aplicație.
Date de antrenament
După cum s-a discutat anterior, în timpul procesului de antrenament furnizăm rețelei imagini etichetate cu clasele de obiecte corespunzătoare, cum ar fi automobile, nave etc. Pentru exemplul prezentat, a fost utilizat setul de date CIFAR-10 deja disponibil.
În practică, inteligența artificială poate fi utilizată pentru mult mai mult decât recunoașterea pisicilor, câinilor sau automobilelor. De exemplu, dacă trebuie dezvoltată o aplicație pentru detectarea calității șuruburilor într-un proces de fabricație, rețeaua trebuie antrenată cu imagini care conțin atât șuruburi conforme, cât și defecte. Crearea unui astfel de set de date poate fi extrem de laborioasă și consumatoare de timp și reprezintă adesea cea mai costisitoare etapă în dezvoltarea unei aplicații AI.
Odată ce setul de date a fost creat, acesta este împărțit în date de antrenament și date de testare. Datele de antrenament sunt utilizate pentru instruirea rețelei, așa cum s-a descris anterior, iar datele de testare sunt utilizate la finalul procesului de dezvoltare pentru a verifica funcționalitatea și precizia rețelei antrenate.
Concluzie
În prima parte a acestei serii am prezentat conceptele de bază ale rețelelor neurale și am analizat structura și funcționarea unei rețele neurale convoluționale. În acest articol am explicat modul în care sunt determinate ponderile și biasurile necesare pentru ca o rețea neurală să funcționeze corect, prin procesul de antrenare. Odată ce acești parametri au fost definiți, rețeaua este capabilă să generalizeze și să efectueze recunoașterea obiectelor pentru date noi.
În partea a 3-a a acestei serii, vom testa rețeaua neurală pentru recunoașterea pisicilor prin implementarea sa în hardware. În acest scop, vom utiliza microcontrolerul MAX78000 care integrează un accelerator CNN bazat pe hardware, dezvoltat de Analog Devices.
Autor: Ole Dreessen, Staff Engineer, Field Applications, Analog Devices
Vizitați https://ez.analog.com
![]()
Glosar de termeni
- Rețea neurală convoluțională (CNN) – Tip de rețea neurală special concepută pentru procesarea datelor structurate spațial, precum imaginile, folosind straturi de convoluție și filtrare.
- Antrenare (training) – Procesul prin care o rețea neurală își ajustează parametrii interni (ponderi și biasuri) pe baza datelor de intrare și a valorilor țintă.
- Funcție de pierdere (loss function) – Funcție matematică ce cuantifică diferența dintre rezultatul produs de rețea și valoarea țintă dorită; este utilizată pentru optimizarea parametrilor rețelei.
- Feedforward – Etapa în care datele de intrare sunt propagate prin rețea pentru a produce o ieșire, fără ajustarea parametrilor.
- Propagare înapoi (backpropagation) – Algoritm utilizat pentru ajustarea ponderilor și biasurilor prin propagarea erorii de la ieșire către straturile anterioare.
- Gradient – Vector matematic care indică direcția și rata maximă de variație a unei funcții; utilizat pentru optimizarea funcției de pierdere.
- Metoda de coborâre a gradientului – Algoritm de optimizare care ajustează parametrii rețelei prin pași succesivi în direcția reducerii funcției de pierdere.
- Supraajustare (overfitting) – Situație în care rețeaua învață prea bine datele de antrenament, dar nu reușește să generalizeze pentru date noi.
- Subajustare (underfitting) – Situație în care modelul este prea simplu pentru a capta structura datelor, rezultând performanțe slabe.
- Date de antrenament / date de testare – Seturi de date utilizate, respectiv, pentru instruirea rețelei și pentru evaluarea performanței acesteia.