Când DCT (Transformarea Cosinus Discretă) este aplicată unui grup de 8 x 8 pixeli, rezultatele apar într-un spectru de 8 x 8 valori. Cu alte cuvinte, 64 de numere sunt schimbate cu alte 64 de numere. Toate aceste valori sunt reale. Ca şi la analizele Fourier, fiecare valoare din spectru este amplitudinea unei funcţii de bază. Funcţiile de bază ale DCT-ului 8 x 8 sunt date de formula din figura 4.
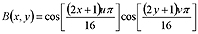
Variabilele x şi y sunt indecşi în domeniul spaţial, iar u şi v sunt indecşi în domeniul frecvenţă. Pentru un DCT de 8 x 8, indecşii variază între 0 şi 7. Cele mai mici frecvenţe apar în colţul stânga-sus al spectrului, în timp ce frecvenţele înalte apar în colţul jos-dreapta. Componenta DC (Direct current = componenta continuă) este la [0,0], valoarea cea mai din stânga-sus. Funcţia de bază pentru [0,1] este un semiciclu al unei funcţii cos într-o direcţie şi o valoare constantă în cealaltă direcţie. Funcţia de bază pentru [1,0] este similară, dar rotită cu 90O.
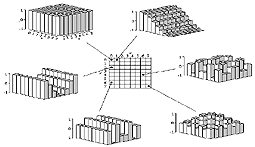
Spectrul DCT constă dintr-o arie de 8 x 8, fiecare element din arie având o amplitudine egală cu una din cele 64 funcţii de bază. Şase din aceste funcţii de bază sunt arătate în figura 5, cu precizarea locului în cadrul matricei spectrale în care apare amplitudinea corespunzătoare.
DCT calculează spectrul prin corelarea grupului de pixeli 8 x 8 cu fiecare din funcţiile de bază. Aceasta înseamnă că fiecare valoare spectrală este găsită prin înmulţirea funcţiei de bază corespunzătoare cu grupul de 8 x 8 pixeli şi apoi adunând rezultatele. Două aproximări sunt apoi necesare pentru a termina calcularea DCT. Mai întâi, se împart la doi cele 15 valori spectrale din coloana zero şi rândul zero, apoi se împart toate cele 64 valori din spectru la 16.
Transformarea inversă DCT este calculată prin asignarea fiecărei amplitudini din spectru unei funcţii de bază corespunzătoare şi adunându-le pentru a reface domeniul spaţial. În funcţie de numărul de biţi utilizaţi pentru reprezentarea unei componente spectrale, refacerea imaginii originale, în domeniul spaţial, este mai mult sau mai puţin afectată de erori. Prin scăderea imaginii refăcute din imaginea originală, rezultă o matrice a erorilor care poate defini un prag acceptat pentru numărul de biţi cu care se reprezintă componentele spectrale. Acesta ar fi primul pas al codării JPEG.
Următorul pas de compresie este acela de renunţare la unele dintre cele 64 de valori spectrale. După cum este cunoscut din analiza unui semnal de imagine, aproape toată energia semnalului este conţinută în componentele de joasă frecvenţă. Aceasta înseamnă că pot fi eliminate componentele de frecvenţă înaltă, fără o deformare semnificativă a semnalului original. Figura 6 exemplifică distorsiunile ce apar în imaginea refăcută, pentru situaţii în care se renunţă la un anumit număr de componente spectrale, din zona frecvenţelor înalte. Grupul 8 x 8 folosit în acest exemplu reprezintă imaginea ochiului din figura 2.
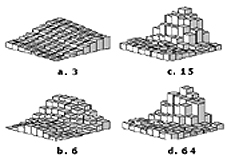
Figura 6 (d) arată refacerea completă prin folosirea celor 64 valori spectrale. Celelalte figuri arată refacerea imaginii folosind alţi coeficienţi de reducere a valorilor spectrale.
Comparând figura 6 (c) cu 6 (d) rezultă că prin reducerea a 3/4 din numărul componentelor spectrale de înaltă frecvenţă, eroarea produsă asupra imaginii este destul de mică.
În schemele practice de realizare a compresiei JPEG, reducerea numărului de biţi cu care sunt reprezentate componentele spectrale şi eliminarea unor componente spectrale are loc într-un singur pas, controlat de un tabel de cuantizare. Două exemple de tabele de cuantizare, pentru compresie joasă şi înaltă, sunt arătate în figura 7.

Fiecare valoare din spectru este divizată cu valoarea corespunzătoare din tabelul de cuantizare şi rezultatul este rotunjit la cel mai apropiat întreg. De exemplu, valoarea din stânga-sus a tabelului de cuantizare este unu (1), rezultând că valoarea DC este lăsată neschimbată. În comparaţie cu aceasta, valoarea din dreapta-jos din figura 7 (a) este 16, ceea ce înseamnă că domeniul original de -127 … +127 este redus la numai -7 … +7. Cu alte cuvinte, valoarea a fost redusă în precizie de la 8 biţi până la 4 biţi. Într-un caz extrem, valoarea din dreapta-jos din figura 7 (b) este 256, eliminând astfel complet valoarea spectrală.
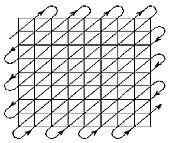
Următorul pas al codării JPEG îl reprezintă transformarea spectrului modificat într-o secvenţă liniară, prin baleierea în zigzag a datelor obţinute, aşa cum se arată în figura 8, pentru a plasa împreună toate componentele de înaltă frecvenţă la sfârşitul secvenţei liniare. Urmează două compresii succesive ale şirului de date astfel obţinut, denumite Run-length (prin care se scurtează şirurile ce conţin date ce se repetă) şi Huffman (în care se utilizează probabilităţile de apariţie ale unei anumite valori, în procesul de compresie). Deşi procesul de compresie JPEG este realizat hard, unii parametri de compresie pot fi schimbaţi în cursul conversiei. Mai mult spus, utilizatorul unui aparat de fotografiat numeric, face această schimbare prin selectarea fie a rezoluţiei fotografiei realizate fie a numărului de poziţii filmate, evident cu pierderea de calitate corespunzătoare.

În figura 9 este prezentată aceeaşi imagine, obţinută prin compresie JPEG, cu rate diferite de compresie, 3/1, 7/1 şi 45/1. Pierderea de calitate este evidentă pentru ultima imagine, în care fiecare din grupele 8 x 8 sunt reprezentate prin aproximativ 12 biţi.
Înainte de a încheia această scurtă prezentare a standardului JPEG voi mai face două precizări şi anume:
• în echipamentele în care compresia JPEG a imaginii trebuie să se facă în timp real, acest lucru se realizează hard, adică tot algoritmul prezentat mai sus se implementează constructiv, într-un circuit integrat de foarte mare complexitate. Este şi cazul aparatelor de fotografiat numerice, al căror preţ încă mare pentru utilizatorul casnic, este dat şi de existenţa acestui circuit;
• în calculatoarele în care prelucrarea informaţiei codificate JPEG nu se mai produce în timp real, decodificarea sau codificarea JPEG se face soft, adică cu programe. Sistemele de operare cât şi mediile de programare care lucrează frecvent cu imagini au module puternice de prelucrare JPEG a imaginilor.
– continuare din numărul trecut –
Ing. Toader Melinte
S.C.Seektron S.R.L
Tel. 0244-185920
melin@xnet.ro
www.seektron.ro

