LTspice® poate fi utilizat pentru a efectua o analiză statistică a toleranței pentru circuite complexe. Acest articol va prezenta tehnici de analiză a toleranței folosind distribuțiile Monte Carlo și Gaussiană și analiza cazului cel mai defavorabil în LTspice. Pentru a demonstra eficacitatea metodei, un circuit, de exemplu de stabilizare a tensiunii, este modelat în LTspice, demonstrând tehnicile de distribuție Monte Carlo și Gaussiană pentru referința de tensiune internă și rezistorii de reacție. Rezultatele acestei simulări sunt comparate cu o simulare de analiză a cazului cel mai defavorabil. Sunt incluse patru anexe. Anexa A oferă informații privind distribuția referințelor de tensiune ajustate. Anexa B oferă o analiză a distribuției Gaussiene în LTspice. Anexa C oferă o vizualizare grafică a distribuției Monte Carlo, așa cum este definită de LTspice. Anexa D oferă instrucțiuni pentru editarea schemelor LTspice și extragerea datelor simulate.
Acest articol ilustrează analiza statistică ce poate fi efectuată cu LTspice. Articolul nu este o trecere în revistă a principiilor de proiectare 6-sigma, a teoremei limitei centrale sau a eșantionării Monte Carlo.
Analiza toleranței
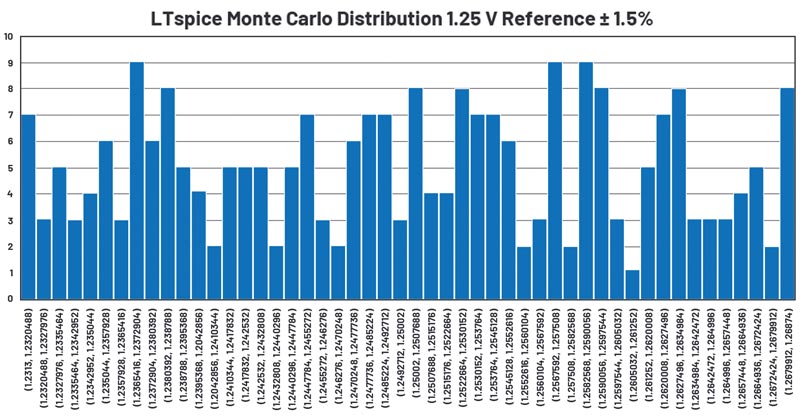
Figura 2: Rezultatele simulării Monte Carlo sub forma unei histograme a referinței de 1,25 V, 50 de bare, 251 de puncte.
În proiectarea sistemelor, trebuie luate în considerare constrângerile de toleranță parametrică pentru a asigura o proiectare reușită. O abordare obișnuită utilizează analiza cazului cel mai defavorabil (WCA) în care toți parametrii sunt ajustați la limita maximă de toleranță. Într-o analiză a cazului cel mai defavorabil, performanța sistemului este analizată pentru a determina dacă rezultatul în cel mai defavorabil caz se încadrează în specificațiile de proiectare a sistemului. Există limitări ale eficacității WCA, cum ar fi:
- WCA necesită determinarea parametrilor care trebuie să fie maximizați sau minimizați pentru un rezultat real în cel mai rău caz.
- Rezultatele WCA încalcă adesea cerințele specificațiilor de proiectare, ceea ce duce la o selecție costisitoare a componentelor pentru a obține rezultate acceptabile.
- Rezultatele WCA nu reprezintă, din punct de vedere statistic, rezultate observate în mod obișnuit; pentru a observa un sistem care prezintă performanțe WCA, poate fi necesar un număr foarte mare de sisteme asamblate.
O abordare alternativă pentru analiza toleranței sistemului este utilizarea instrumentelor statistice pentru analiza toleranței componentelor. Avantajul unei analize statistice este că datele rezultate au o distribuție care reflectă ceea ce ar trebui să fie măsurat în mod obișnuit în sistemele fizice. În acest articol, LTspice este utilizat pentru a simula performanța circuitelor cu distribuții Monte Carlo și Gaussiană aplicate la variația toleranței parametrice. Acest lucru este comparat cu o simulare WCA.
În ciuda problemelor observate cu WCA, atât analiza în cel mai defavorabil caz, cât și analiza statistică oferă informații valoroase pentru proiectarea sistemelor. Pentru un tutorial foarte util privind aplicarea WCA cu ajutorul LTspice, consultați “LTspice: Worst-Case Circuit Analysis with Minimal Simulations Runs” de Gabino Alonso și Joseph Spencer.
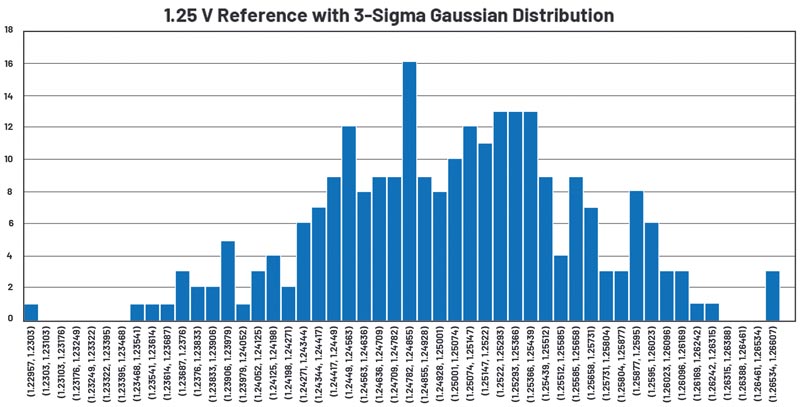
Figura 4: Rezultatele simulării Gaussiene 3-sigma ca histogramă a referinței de 1,25V, 50 de bare, 251 de puncte.
Distribuția Monte Carlo
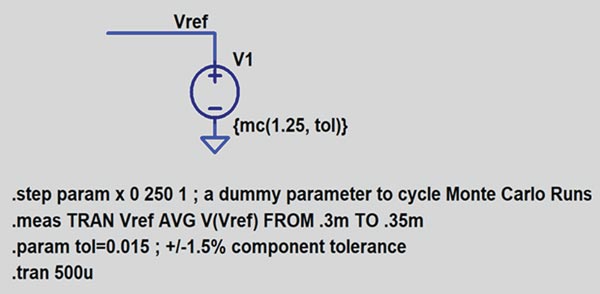
Figura 1 prezintă o referință de tensiune modelată în LTspice cu o distribuție Monte Carlo. Sursa de tensiune are valoarea nominală de 1,25V, iar toleranța este de 1,5%. Distribuția Monte Carlo definește 251 de stări de tensiune în intervalul de toleranță de 1,5%. Figura 2 prezintă histograma celor 251 de valori cu 50 de bare. Tabelul 1 ilustrează statisticile asociate ale distribuției.
| Rezultat | |
| Medie | 1.249933 |
| Minim | 1.2313 |
| Maxim | 1.26874 |
| Deviația standard | 0.010615 |
| Eroare pozitivă | 1.014992 |
| Eroare negativă | 0.98504 |
Tabelul 1: Analiza statistică a rezultatelor simulării Monte Carlo
Distribuția Gaussiană
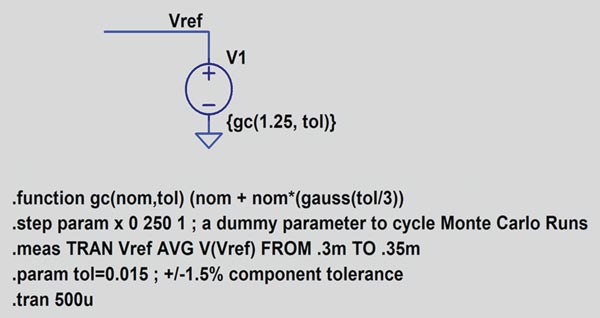
Figura 3 prezintă o referință de tensiune modelată în LTspice cu o distribuție Gaussiană. Sursa de tensiune are valoarea nominală de 1,25V, iar toleranța este de 1,5%. Distribuția Gaussiană definește 251 de stări de tensiune în intervalul de toleranță de 1,5%. Figura 4 prezintă histograma celor 251 de valori cu 50 de bare. Tabelul 2 ilustrează statisticile asociate ale distribuției.
| Rezultat | |
| Minim | 1.22957 |
| Maxim | 1.26607 |
| Medie | 1.25021 |
| Deviația standard | 0.006215 |
| Eroare pozitivă | 1.012856 |
| Eroare negativă | 0.983656 |
Tabelul 2: Analiza statistică a rezultatelor simulării referinței Gaussiene
Distribuțiile Gaussiene sunt distribuții normale cu o curbă în formă de clopot și cu densitatea de probabilitate prezentată în figura 5.
Corelația dintre distribuțiile Gaussiene ideale și cele simulate de LTspice este prezentată în tabelul 3.
| Simulată | Ideală | |
| Împrăștiere 1-Sigma | 67.73% | 68.27% |
| Împrăștiere 2-Sigma | 95.62% | 95.45% |
| Împrăștiere 3-Sigma | 99.60% | 99.73% |
Tabelul 3: Distribuția statistică a distribuției Gaussiene simulate de 251 puncte LTspice
Pentru a rezuma simulările de mai sus, LTspice poate fi utilizat pentru a simula o distribuție de toleranță Gaussiană sau Monte Carlo pentru o sursă de tensiune. Această sursă de tensiune poate fi utilizată pentru a modela o referință într-un convertor DC-DC. Simularea LTspice a distribuției Gaussiene LTspice se potrivește îndeaproape cu distribuția densității de probabilitate prezisă.
Analiza toleranței pentru simularea unui convertor DC-DC
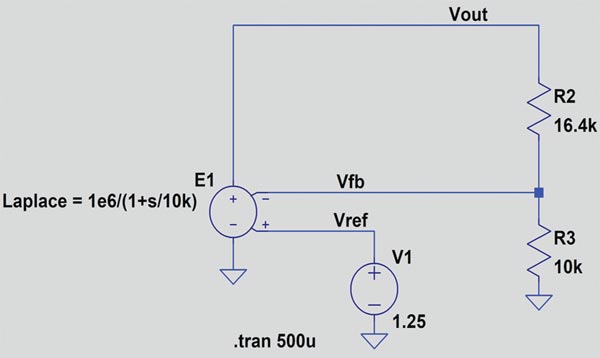
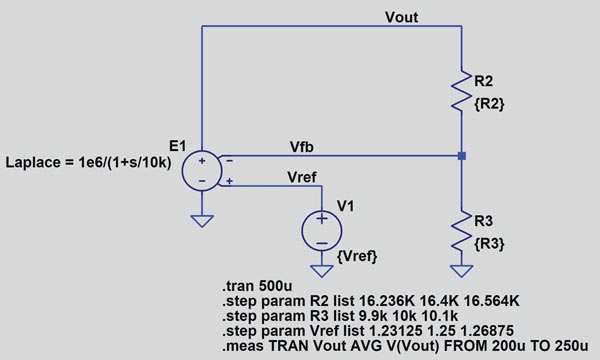
Figura 6 este o schemă de simulare LTspice pentru un convertor DC-DC care utilizează o sursă de tensiune controlată pentru a modela reacția de tensiune în buclă închisă. Valorile nominale ale rezistorilor de reacție R2 și R3 sunt de 16,4 kΩ și 10 kΩ. Valoarea nominală a tensiunii interne de referință este de 1,25V. În acest circuit, valoarea nominală a tensiunii stabilizate, VOUT, sau punctul de referință este de 3,3V.
Pentru a simula analiza de toleranță a stabilizatorului de tensiune, rezistorii de reacție R2 și R3 sunt definiți cu o toleranță de 1%, iar referința de tensiune internă este definită cu o toleranță de 1,5%. În această secțiune vor fi prezentate trei metode de analiză a toleranței: analiza statistică utilizând o distribuție Monte Carlo, analiza statistică utilizând o distribuție Gaussiană și o analiză a cazului cel mai defavorabil (WCA).
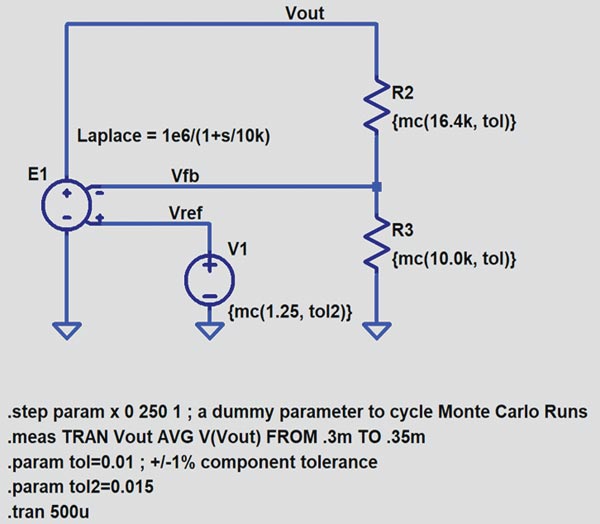
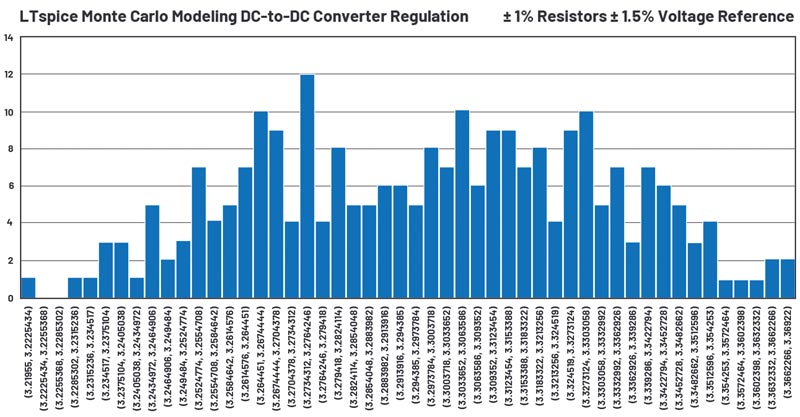
Figurile 7 și 8 ilustrează schema și histograma stabilizatorului de tensiune pentru o simulare care utilizează distribuții Monte Carlo.
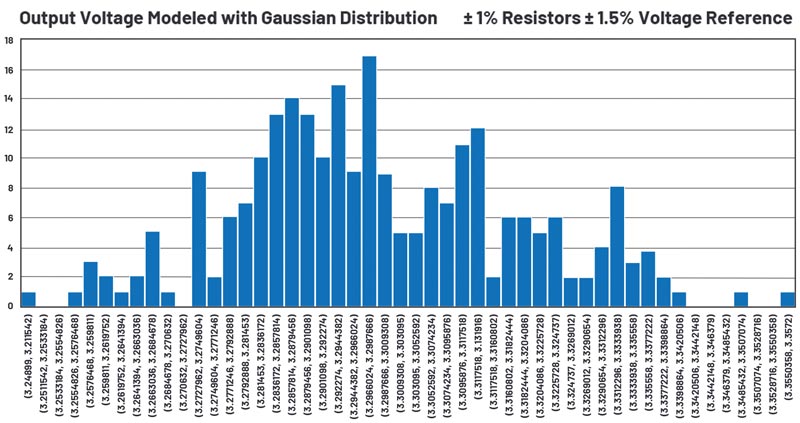
Figurile 9 și 10 ilustrează schema și histograma stabilizatorului de tensiune pentru o simulare care utilizează distribuții Gaussiene.
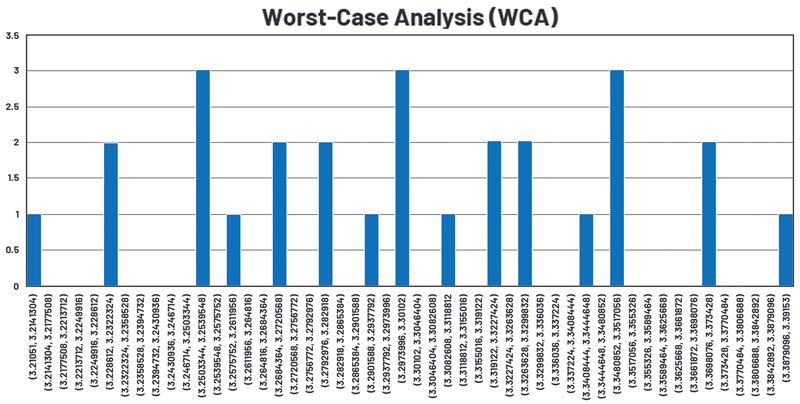
Figurile 11 și 12 ilustrează schema și histograma stabilizatorului de tensiune pentru o simulare care utilizează WCA.
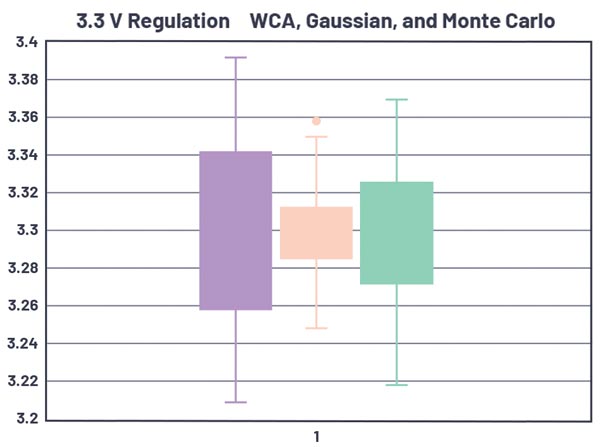
Tabelul 4 și figura 13 compară rezultatele analizei toleranței. În acest exemplu, WCA prezice cea mai mare abatere maximă, iar simularea bazată pe o distribuție Gaussiană o prezice pe cea mai mică. Acest lucru este ilustrat în figura 13 într-o diagramă de tip “box and whisker” – zona solidă reprezintă limita 1-sigma, în timp ce liniile subțiri (sau mustăți) reprezintă valorile minime și maxime.
| WCA | Gaussiană | Monte Carlo | |
| Medie | 3.30013 | 3.29944 | 3.29844 |
| Minim | 3.21051 | 3.24899 | 3.21955 |
| Maxim | 3.39153 | 3.35720 | 3.36922 |
| Deviația standard | 0.04684 | 0.01931 | 0.03293 |
| Eroare pozitivă | 1.02774 | 1.01733 | 1.02098 |
| Eroare negativă | 0.97288 | 0.98454 | 0.97562 |
Tabelul 4: Rezumatul statistic al stabilizatorului de tensiune pentru cele trei metode de analiză a toleranței
Rezumat
Utilizând un model simplificat de convertor DC-DC, au fost analizate trei variabile: doi rezistori de reacție și referința de tensiune internă, care au fost utilizate pentru a modela ajustarea tensiunii VOUT. Utilizând analiza statistică, este prezentată distribuția rezultată a punctului de setare a tensiunii. Rezultatele sunt reprezentate grafic. Acestea sunt comparate cu un calcul în cazul cel mai defavorabil. Datele rezultate ilustrează faptul că limitele cazului cel mai defavorabil sunt improbabile din punct de vedere statistic.
Aprecieri
Simulările au fost efectuate în LTspice.
Graficele și reprezentările grafice au fost realizate în Excel.
Mulțumim mai multor colaboratori anonimi din cadrul Analog Devices și lui David Rick de la Hach, pentru îndrumarea și informațiile primite în legătură cu acest articol.
Anexa A
Anexa A este o introducere în distribuția statistică a referințelor de tensiune ajustate în circuitele integrate.
Referințele interne sunt Gaussiene înainte de a fi ajustate și Monte Carlo după ajustare. Procesul de ajustare este, de obicei, după cum urmează:
• Se măsoară valoarea anterioară ajustării. Distribuția este de obicei Gaussiană.
• Poate fi ajustată această unitate? Dacă nu, eliminați unitatea. Această etapă constă, în esență, în tăierea “cozilor” distribuției Gaussiene.
• Ajustați valoarea. Acest lucru deplasează tensiunea de referință cât mai aproape posibil de cea ideală; valorile care sunt cele mai îndepărtate de cea ideală sunt deplasate cel mai mult. Rezoluția de ajustare este totuși foarte fină, astfel încât valorile de referință care sunt apropiate de ideal nu sunt deplasate.
• Măsurați valoarea după ajustare și fixați-o dacă este în regulă.
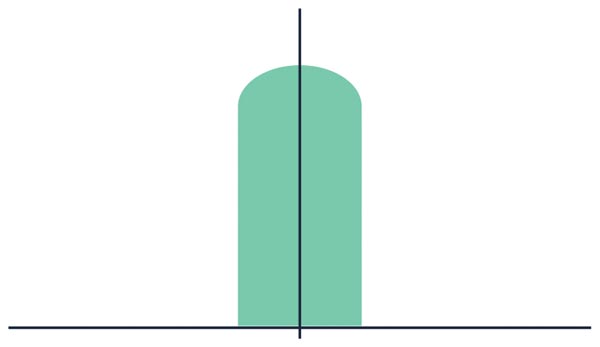
Distribuția rezultată are unele valori neschimbate față de distribuția Gaussiană originală, în timp ce altele sunt îngrămădite cât mai aproape de ideal. Histograma rezultată seamănă cu o coloană cu o cupolă în partea superioară, așa cum este ilustrat în figura 14.
Deși aceasta pare mai degrabă o distribuție aleatorie, nu este așa. În cazul în care produsul este ajustat după încapsulare, distribuția la temperatura camerei va arăta ca în figura 14. Dacă produsul este ajustat la sortarea pastilei de siliciu, montarea într-o capsulă de plastic face ca distribuția de mai sus să se răspândească din nou. Rezultatul este, de obicei, o distribuție Gaussiană deformată.
Anexa B
Anexa B este o scurtă trecere în revistă a comenzii de distribuție Gaussiană oferită în LTspice. Se va face o trecere în revistă a distribuțiilor sigma = 0,00333 și sigma = 0,002 și se vor face câteva comparații numerice între distribuțiile Gaussiene ideale și cele simulate. Intenția acestei anexe este de a oferi o afișare grafică și o analiză numerică a rezultatelor simulării.
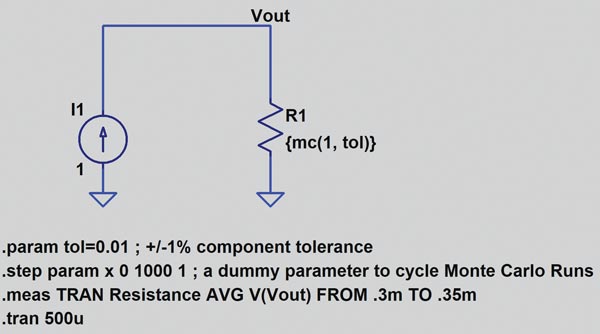
Figura 15 este o schemă pentru o distribuție Gaussiană în 1001 de puncte pentru rezistorul R1.
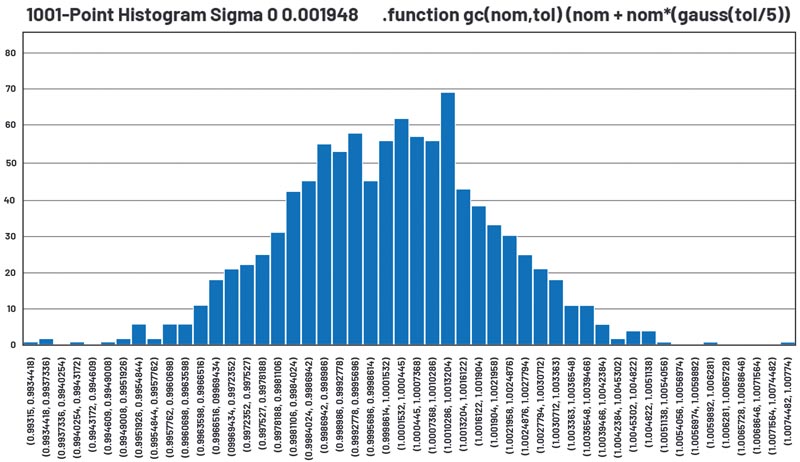
De interes este modificarea instrucțiunii .function pentru a defini funcția Gaussiană cu tol/5. Astfel, abaterea standard va fi de 0,002, sau 1⁄5 din toleranța de 1%. Histograma este reprezentată în figura 16.
Tabelul 5 prezintă analiza statistică a simulării în 1001 de puncte. De interes este deviația standard de 0,001948, în comparație cu 0,002 așteptat.
| Rezultat | |
| Medie | 1.000049 |
| Deviația standard | 0.001948 |
| Minim | 0.99315 |
| Maxim | 1.00774 |
| Mediană | 1.00012 |
| Mod | 1.00024 |
| Puncte în limita a 1 Sigma | 690 (68.9%) |
Tabelul 5: Statistici pentru distribuția simulată 5-Sigma
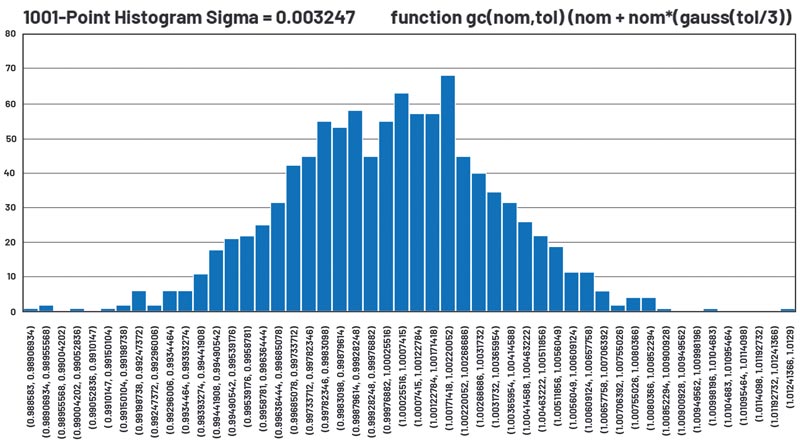
Rezultate similare sunt prezentate în figura 17 și în tabelul 6 pentru sigma = 0,00333 sau 1⁄3 din toleranța definită ca fiind de 1 %.
| Rezultat | |
| Medie | 1.000080747 |
| Deviația standard | 0.003247278 |
| Minim | 0.988583 |
| Maxim | 1.0129 |
| Mediană | 1.0002 |
| Mod | 1.00197 |
| Puncte în limita a 1 Sigma | 690 (68.93%) |
Tabelul 6: Statistici pentru distribuția Gaussiană simulată 3-sigma
Anexa C
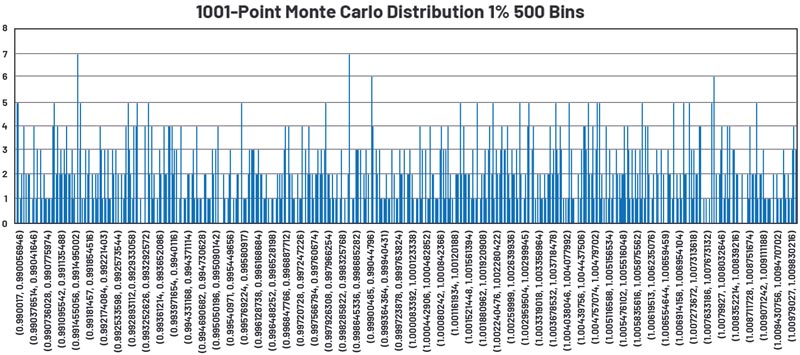
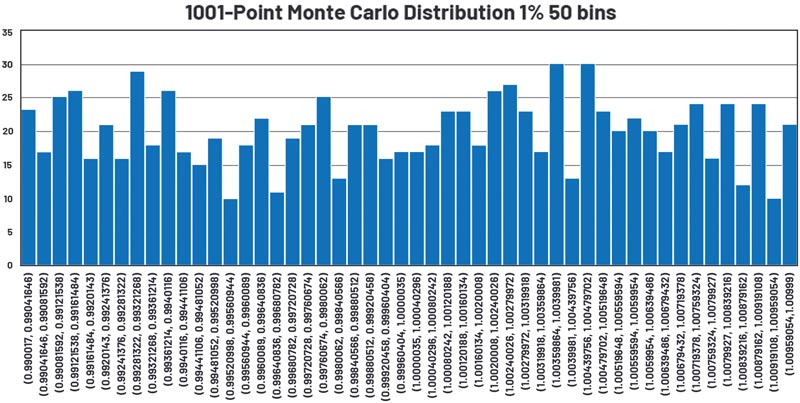
Figura 18 până la figura 21 și tabelul 7 reprezintă o schemă pentru o simulare Monte Carlo în 1001 de puncte.
| Rezultat | |
| Medie | 1.000014 |
| Minim | 0.990017 |
| Maxim | 1.00999 |
| Deviația stadard | 0.005763 |
| Mediană | 1.00044 |
| Mod | 1.00605 |
Tabelul 7: Analiza statistică a distribuției Monte Carlo simulate prezentate în figura 18 până la figura 21
Anexa D
Anexa D analizează modul cum să:
- Editați schema LTspice pentru a activa analiza toleranței și să
- Utilizați comanda .measure și jurnalul de erori SPICE.
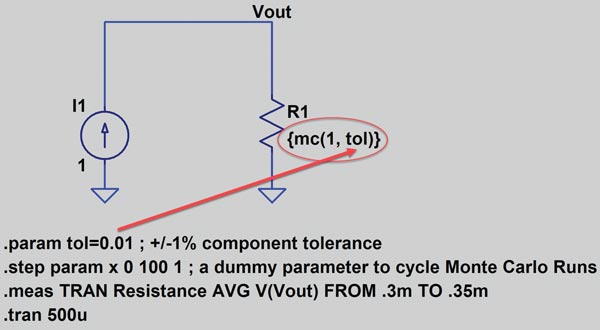
Figura 22 ilustrează schema pentru analiza de toleranță Monte Carlo. Săgeata roșie indică faptul că toleranța pentru componentă este definită în instrucțiunea .param. Instrucțiunea .param este o directivă SPICE.
Valoarea rezistenței lui R1 poate fi editată făcând clic dreapta pe componentă. Acest lucru este prezentat în figura 23.
Introducând {mc(1, tol)} se definește valoarea nominală a rezistenței ca fiind 1 cu o distribuție Monte Carlo definită de parametrul tol. Parametrul tol este definit ca o directivă SPICE.
Introducerea directivei SPICE prezentată în figura 22 se poate face făcând clic pe SPICE Directive (Directiva SPICE) din bara de control. Aceasta este ilustrată în figura 24.
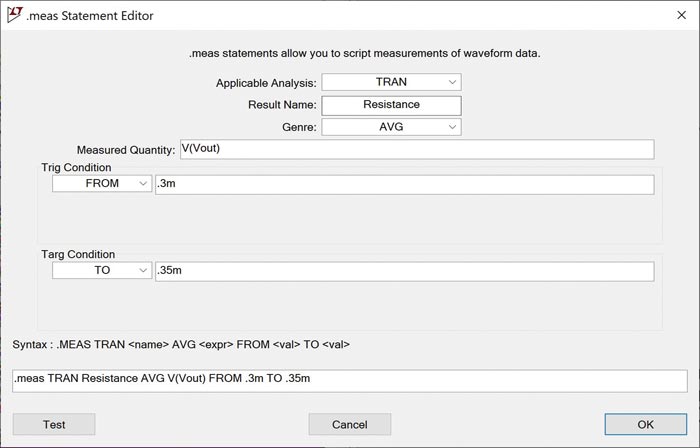
Comanda .meas dispune de o interfață grafică foarte utilă pentru introducerea parametrilor de interes. Aceasta este ilustrată în figura 25. Pentru a accesa această interfață grafică, introduceți directiva SPICE ca o comandă .meas. Faceți clic dreapta pe comanda .meas și se va deschide GUI.
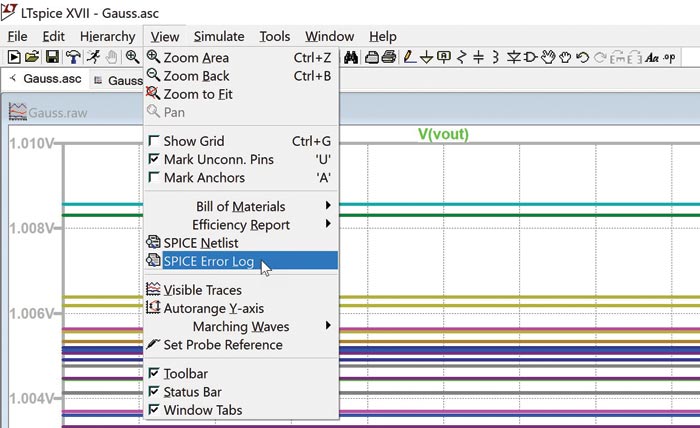
Datele măsurate sunt înregistrate în SPICE Error Log (Jurnalul de erori SPICE). Figurile 26 și 27 sunt două ilustrații care arată cum se accesează SPICE Error Log.
Acesta poate fi, de asemenea, accesat direct din schemă, făcând clic dreapta pe schemă, așa cum se arată în figura 27.
Deschiderea jurnalului de erori SPICE prezintă valorile măsurate, după cum se arată în figura 28. Acestea pot fi copiate și plasate în Excel pentru analiză numerică și grafică.
Autor: Steve Knudtsen, Field Applications Engineer
Despre autor
Steve Knudtsen este inginer senior de aplicații la Analog Devices, cu sediul în Colorado. A absolvit Universitatea de Stat din Colorado cu o diplomă de licența în inginerie electrică și lucrează la Linear Technology (acum Analog Devices) din 2000. Poate fi contactat la steve.knudtsen@analog.com.